Soluciones Algebra Lineal y sus Aplicaciones - Linear Algebra and its Applications - 4ed David Lay : Linear Algebra - David Lay - 4ed Solutions

En los ejercicios 1 a 4, obtenga los valores singulares de las matrices

Get 7.4.4 exercise solution

En los ejercicios 5 a 12, encuentre una DVS para cada matriz. [Sugerencia: En el ejercicio 11, una elección para U es

En el ejercicio 12, una columna de U puede ser

Get 7.4.5 exercise solution

Get 7.4.6 exercise solution

Get 7.4.7 exercise solution

Get 7.4.8 exercise solution

Get 7.4.9 exercise solution

Get 7.4.10 exercise solution

Get 7.4.11 exercise solution

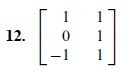
Get 7.4.12 exercise solution

13. Encuentre la DVS de

Get 7.4.13 exercise solution

14. En el ejercicio 7, obtenga un vector unitario x en el cual Ax tiene longitud máxima.
Get 7.4.14 exercise solution

15. Suponga que la siguiente factorización es una DVS de una matriz A, con las entradas en U y V redondeadas a dos decimales

) ¿Cuál es el rango de A? b) Utilice esta descomposición de A, sin hacer cálculos, y escriba una base para Col A y una base para Nul A. [Sugerencia: Primero escriba las columnas de V].
Get 7.4.15 exercise solution

16. Repita el ejercicio 15 para la siguiente DVS de una matriz A de 3 x 4:

Get 7.4.16 exercise solution

En los ejercicios 17 a 24, A es una matriz de m n con una descomposición en valores singulares A= UEVT, donde U es una matriz ortogonal de m x m, e es una matriz “diagonal” de m x n con r entradas positivas y sin entradas negativas, y V es una matriz ortogonal de n x n. Justifique sus respuestas.

17. Suponga que A es cuadrada e invertible. Encuentre una descomposición en valores singulares de A -1.
Get 7.4.17 exercise solution

18. Demuestre que si A es cuadrada, entonces | det A| es el producto de los valores singulares de A.
Get 7.4.18 exercise solution

19. Demuestre que las columnas de V son vectores propios de ATA, que las columnas de U son vectores propios de AAT, y que las entradas diagonales de E son los valores singulares de A. [Sugerencia: Utilice la DVS para calcular ATA y AAT].
Get 7.4.19 exercise solution

20. Demuestre que si A es una matriz positiva definida de n n, entonces una diagonalización ortogonal A PDPT es una descomposición en valores singulares de A.
Get 7.4.20 exercise solution

21. Demuestre que si P es una matriz ortogonal de m m, entonces PA y A tienen los mismos valores singulares.
Get 7.4.21 exercise solution

22. Justifique el enunciado del ejemplo 2 referente a que el segundo valor singular de una matriz A es el máximo de || Ax|| conforme x varía sobre todos los vectores unitarios ortogonales a v1, siendo v1 un vector singular derecho correspondiente al primer valor singular de A. [Sugerencia: Utilice el teorema 7 de la sección 7.3].
Get 7.4.22 exercise solution

23. Sean U = [u1... um] y V = [v1...vn], donde uj y vj son como en el teorema 10. Demuestre que

Get 7.4.23 exercise solution

24. Utilizando la notación del ejercicio 23, demuestre que ATuj <= sjvj para 1 <= j<= r =rango A.
Get 7.4.24 exercise solution

25. Sea T : Rn --> R m una transformación lineal. Describa cómo encontrar una base B para Rn y una base C para Rm tal que la matriz para T respecto de B y C sea una matriz “diagonal” de m x n.

Get 7.4.25 exercise solution

[M] Calcule una DVS para cada matriz en los ejercicios 26 y 27. Informe las entradas matriciales finales con dos decimales. Utilice el método de los ejemplos 3 y 4.

Get 7.4.26 exercise solution

Get 7.4.27 exercise solution

28. [ M] Determine los valores singulares de la matriz de 4 x 4 en el ejercicio 9 de la sección 2.3, y calcule el número de condición o1 /o4.
Get 7.4.28 exercise solution

29. [ M] Calcule los valores singulares de la matriz de 5 x 5 en el ejercicio 10 de la sección 2.3, y determine el número de condición o1/ o5.
Get 7.4.29 exercise solution

Linear Algebra - David Lay - 4ed Solutions - Chapter 7. Section 7.4 Solutions